Application of Comprehensive Index Method in Teaching Performance Evaluation of University Teachers
-
摘要:
目的 分析基于优序图法的综合指数法评价高校教师教学水平，为今后教研室评价教师的综合教学水平提供参考。 方法 选择课堂教学质量评分、教研室教学活动参与率、课程考核管理3方面，包括3个一级指标9个二级指标组成指标评价体系，运用优序图法确定指标权重，采用综合指数法综合评价教学水平。 结果 优序图法确定课堂教学质量评分、教研室教学活动参与率、课程考核管理的权重分别为0.42、0.22、0.36，综合指数法评价教研室B1-B7共7位教师的教学水平综合指数值依次为1.19、1.11、1.46、0.94、0.99、0.90、1.01，从高到低的排名为B3 > B1 > B2 > B7 > B5 > B4 > B6。 结论 基于优序图法的综合指数法消除不同指标性质不同和计量单位不同的影响，加入各指标的权重，结果得出各个教师多方面的综合表现，且方法简单易行，可应用于教研室对高校教师综合教学水平的评价。 Abstract:Objective This paper analyzes the evaluation of the teaching performance of university teachers by the comprehensive index method based on the superior order graph method, and provides reference for the future evaluation of the comprehensive teaching performance of teachers by the teaching and research section. Methods The evaluation system includes three aspects: classroom teaching quality rating, teaching activity participation rate of teaching and research section and course assessment management. The index evaluation system consists of 3 first-level indexes and 9 second-level indexes. The index weight is determined by using the superior order diagram method, and the comprehensive index method is used to comprehensively evaluate the teaching level. Results The weights of classroom teaching quality rating, teaching activity participation rate and course assessment management determined by the optimal sequence diagram were 0.42, 0.22 and 0.36, respectively. The comprehensive index method was used to evaluate the teaching level of 7 teachers from B1-B7 in the teaching and research section. The comprehensive index values were 1.19, 1.11, 1.46, 0.94, 0.99, 0.90, 1.01, and the ranking from high to low was B3 > B1 > B2 > B7 > B5 > B4 > B6. Conclusion The comprehensive index method based on the optimal sequence diagram methods avoided the influence caused by the difference in properties and units of measurement of various indexes, whole added the weight of each index, so as to obtain the comprehensive performance of each teacher in many aspects. This method is simple and feasible, and can be used in the teaching and research section to evaluate the comprehensive teaching performance of university teachers. -
采用硬膜外镇痛能显著减轻分娩时的疼痛，其对母亲和婴儿的影响微乎其微，且能让产妇保持清晰的意识，积极地参与分娩过程，已成为眼下分娩最普遍采纳的减痛方式之一[1]。同时，此法能有效地提升妇产科服务的水平及孕产妇的感官满意度，并显著减少产后抑郁症状的出现，应广泛推荐使用[2]。传统的分娩镇痛管理方式依赖于孕妇的主动汇报，随后由护士向麻醉医生传达，再由麻醉医生进行处理[3]。这一过程，依赖于护士的积极性，护士积极对待患者能促进疼痛缓解[4]，存在人力成本高、监测及反馈不全面等问题。
随着科技的发展，人工智能（artificial intelligence，AI）飞速发展，将AI引入镇痛领域可能有望开创预防性镇痛是创新镇痛策略的有意义的尝试和起步[5]。现有的智能化信息化管理系统能够记录产妇的各项信息、显示当前镇痛泵的运行参数信息、获取产妇通过疼痛评分软件反馈的数值评定量表（numeric rating scale，NRS）疼痛评分等。这一动态工作体系用于分娩镇痛临床效果确切，能够提高分娩镇痛的管理质量[6]，同时简化麻醉医务人员工作流程，提高工作效率。此外，规范记录患者的疼痛信息，在围术期大数据驱动下的麻醉管理研究势必会发现既往无法发现的内容，从而给手术患者带来更多的益处[7]。本文旨在探讨智能化与信息化管理与传统管理方式在分娩镇痛中的效果对比分析，此研究对分娩镇痛的实际应用具有一定的参考价值。
1. 资料与方法
1.1 研究对象
本研究基于2021年厦门市医疗卫生指导项目（3502Z20214ZD1102），且经厦门市弘爱妇产医院审查委员会批准（AF-SQ-004-01.1）。选取2022年4月至2023年4月在厦门市弘爱妇产医院行200例临产孕妇作为实验对象，将受试者用随机数字分为2组，随机化分组：应用SPSS 27.0软件产生随机号（固定值为20220404），按1∶1的比率，将患者随机分为2组，使用不透光信封进行随机分配方案隐藏，助手按照患者筛选合格的入组顺序依次拆开信封，依据分组代码选择对应的治疗组。A组为研究组（信息化管理组），B组对照组（传统管理组），每组100例，均符合纳入标准和排除标准[6]。
纳入标准：（1）ASA分级（American society of Aneshesiologists physical status classification system）I-II级；（2）年龄22～35岁，体重指数（body mass index，BMI） 22～28 kg/m2；（3）足月妊娠（37～42周）；（4）自愿参加并在麻醉医生告知情况下签署麻醉知情同意书。排除标准：（1）合并高血压、心脏病、困难气道等；（2）有实验相关药物过敏史；（3）合并肿瘤疾病；（4）合并神经系统疾病，精神病史等。剔除标准：操作过程中造成硬膜外穿破，硬膜外导管误操作置入蛛网膜下腔或椎管内血管中，分娩镇痛期间硬膜外导管意外脱落进行重新置管，首次镇痛泵运行脉冲给予首剂量药物后镇痛不明显以及在分娩镇痛期间因各种原因中转剖宫产。
1.2 研究设计
1.2.1 一般资料采集
收集入组患者年龄、妊娠期、身高、体重、体重指数、孕产史（G/P）、胎位（LOA/ROA）、胎儿体重等基本信息。
2组初始分别纳入100例孕产妇。实验组（A组）中，由于紧急胎儿宫内缺氧和头盆不称等因素，有2名孕产妇转为接受剖腹产手术，有2名孕产妇因为置入的导管脱出而需重新穿刺置管，最终该组共收纳了96名待产女性。对照组（B组）中，同样的紧急胎儿宫内缺氧和头盆不称等因素导致3名孕产妇转为接受剖腹产手术；另外有1名孕产妇出现了单侧阻滞，以及1名孕产妇因为置入的导管脱出而需重新穿刺置管，该组共计纳入了95名孕产妇。2组孕产妇在年龄、妊娠期、身高、体重、体重指数、孕产史（G/P）、胎位（LOA/ROA）、胎儿体重等方面的比较差异无统计学意义（P > 0.05），具有可比性，见表1。
表 1 参与者的一般人口学特征[（$ \bar x \pm s$），n（%），n = 191]Table 1. Demographic information of participants [（$ \bar x \pm s$），n（%），n = 191]组别 A组（n=96） B组（n=95） χ2/z/t P 年龄（岁） 28.54 ±4.17 29.26±4.09 0.175 0.229 孕期 （周） 39.64±1.69 39.41±1.54 0.139 0.337 身高（m） 1.62±0.05 1.63±0.05 0.199 0.171 体重（kg） 69.18±6.72 68.76±6.30 0.065 0.655 BMI （kg/m2） 26.30±1.63 25.84±1.75 0.274 0.060 孕史G 2.02±0.81 1.93±0.83 0.116 0.116 产史P 1.00±0.81 0.93±0.83 0.090 0.090 胎位 LOA 52（54.20） 51（53.70） 0.010 1.000 ROA 44（45.80） 44（46.30） 胎儿体重（g） 5937.50 ±550.866020.42 ±575.830.147 0.310 1.2.2 分娩镇痛实施流程
孕产妇入操作间后常规监测心电图（electrocardiogram，ECG）、无创血压（noninvasive-blood-pressure，NBP）、心率（heart-rate，HR）、指末脉搏血氧饱和度（oxygen saturation of blood，SpO2），连续胎心监测。开放上肢静脉，持续输液乳酸钠林格平衡液。产妇进入产房后有镇痛需求即开始实施分娩镇痛，采用连续硬膜外阻滞镇痛方法，选择L 2～L 3椎管间隙，严格按照椎管内穿刺规范操作流程进行硬膜外穿刺，穿刺针斜口朝向头侧，置入硬膜外导管，置管深度统一为9～10 cm，穿刺置管完毕，进行穿刺验证用以排除导管置入血管或蛛网膜下腔，经硬膜外导管注入试验剂量：为1%利多卡因3 mL，观察3～5 min，若孕产妇未发生相关不良反应，连接电子镇痛泵开机运行，首剂量泵注完成后，观察10 min后测量镇痛平面，进行NRS疼痛评分，若镇痛平面低于T 10水平，且NRS疼痛评分≥4分，再次硬膜外注入5 mL药液。镇痛泵的浓度统一为0.1%罗哌卡因+0.375 μg/mL舒芬太尼，袋内200 mL。以患者身高制定维持计划：（1）160 cm以下的孕产妇以首剂量10 mL，维持剂量50 min内脉冲式给药10 mL，单次按压 10 mL，单次按压后锁时30 min；（2）160～170 cm的孕产妇以首剂量10 mL，维持剂量50 min内脉冲式给药8 mL，单次按压 8 mL，单次按压后锁时30 min；（3）170 cm以上的孕产妇以首剂量10 mL，维持剂量50 min内脉冲式给药12 mL，单次按压 12 mL，单次按压后锁时30 min。
平面稳定后，A组采用REHN（Ⅰ）镇痛泵系统，该系统包含电子镇痛泵和镇痛实施控制管理系统。电子镇痛泵是由输液设备以及1次性使用的专配药物容器构建而成。镇痛实施控制管理系统由中控站、病区控制点以及观测平台共同组成，其中观测平台内安装镇痛控制系统的软件。该电子镇痛泵可根据医师预设的参数，实现定量或断续的精确药物脉冲式注入（患者同样可参与调控止痛效果）。中控站与病区控制点为该止痛注射系统的通讯网络枢纽，负责将终端设备，如电子镇痛泵等的数据信息收集后转发至观测平台。观测平台则是分析并处理上传自电子镇痛泵信息的设备，工作人员可以通过该平台对电子镇痛泵的应用进行实时监控。本桌面管理系统的核心职能涵盖：（1）联合医院信息系统以及监控仪器，采集待产妇女的病历纪录、化验数据、生理监测及胎儿心跳跟踪等相关讯息；（2）展示目前电子镇痛泵设备的操作数据，涉及电子镇痛泵运行维持时间、药物使用量、泵设备的操作次数及有效操作频次；（3）搜集孕产妇通过疼痛指数软件提供的NRS疼痛指标；（4）电子化管理分娩镇痛档案、归类汇总数据报告等多种数字文档。待产女性在分娩后镇痛阶段若自身感觉阵痛严重且强烈，麻醉科医生可通过镇痛实施控制管理系统软件反馈（10 min内电子镇痛泵无效按压2次及以上）进行补救方案：（1）首先检查硬膜外导管的刻度与位置，如若出现单侧椎管阻滞或者硬膜外导管脱落并需要进行重新穿刺则将孕产妇将研究中剔除；（2）测试平面，结果阻滞平面不超过T 10的追加1%利多卡因7～10 mL。B组待产女性在分娩后镇痛阶段若自身感觉阵痛严重且强烈，可利用麻醉科医生的不定期巡查以及床边按钮呼唤助产士、再由助产士将情况告知麻醉科医生到场而获得补救方案，方案同A组方案一致。
1.2.3 观察指标
主要指标为进行镇痛处理前、处理15 min后以及子宫口全开时的数值评定量表（NRS）疼痛评分（NRS评分法:“0：无痛”“1～3：轻度疼痛，不影响睡眠”“4～6：中度疼痛，影响睡眠，但仍可睡眠”“7～10：重度疼痛，不能睡眠”），以及实施分娩镇痛措施后数值评定量表（NRS）显示疼痛程度≥7分的患者占比。次要指标包括电子镇痛泵按压次数、电子镇痛泵有效按压次数、主动补救方案比例（通过麻醉科医生不定期巡查和REHN（Ⅰ）镇痛实施控制管理系统反馈获得）、被动补救方案比例（产妇通过床旁按钮呼叫获取）、不良反应（包括恶心呕吐、瘙痒程度、眩晕、尿潴留等）、产妇对分娩镇痛体验的满意度（2：满意、1：较满意、0：不满意）。
1.3 统计学处理
利用R软件版本3.6.3实现数据的统计分析。对计量资料描述采用均数±标准差（$\bar x \pm s $），对计数资料描述采用数量（n）和百分比（%），计量资料比较采用方差分析、独立样本t检验或非参数检验，2组间多个时间点变化采用重复测量方差分析，计数数据则通过卡方检验或Fisher精确概率法比较不同组间的情况。本研究以α = 0.05作为显著性水平，P < 0.05为差异有统计学意义。
2. 结果
2.1 2组孕产妇分娩镇痛期间NRS评分分析
2组孕产妇NRS评分随着分娩镇痛的实施，在镇痛处理前、处理15 min后以及子宫口全开时的NRS评分随着时间变化都有一定程度的降低，具有时间效应（P < 0.01），在2组孕产妇NRS随时间变化的程度具有时间和组间的交换效应，具有可比性（P < 0.01），见表2。与B组比较，A组子宫口全开时的数值评定量表（NRS）疼痛评分均明显降低（P < 0.05）。2组孕产妇进行镇痛处理前、处理15 min后NRS评分差异均无统计学意义（P = 0.26），见图1。A组实施分娩镇痛措施后数值评定量表（NRS）显示疼痛程度≥7分的患者占比明显低于B组[10例（10.4%）vs 24例（25.2%），P < 0.05]。
表 2 2组孕产妇NRS评分随分娩镇痛实施的时间点变化比较Table 2. Comparison of the changes in NRS scores between two groups of parturients at different time points during labor analgesia因变量 效应 Df Sum Sq Mean Sq F P NRS Time 1 91.50 91.54 16.517 < 0.001*** Group 1 12.10 12.06 2.176 0.141 Time:Group 1 49.90 49.87 8.998 0.003** ** P < 0.01； *** P < 0.001。Time指时间变化效应（3个实验时间点的NRS评分变化效应）；Group指组间效应（为不同组组内3个实验时间点NRS变化的效应）；Time:Group指时间和组间交互效应（为不同组3个实验时间点NRS变化的效应）。 
图 1 2组孕产妇分娩镇痛期间NRS评分比较A：分娩镇痛前2组孕产妇NRS评分对比；B：分娩镇痛后15 min 2组孕产妇NRS评分对比；C：2组孕产妇宫口全开时NRS评分对比。**P < 0.01； ***P < 0.001。Figure 1. Comparison of NRS scores between two groups of parturients during labor analgesia2.2 2组孕产妇分娩镇痛期间镇痛泵使用情况及补救措施比例分析
与B组比较，A组被动补救明显减少，主动补救明显增多（P < 0.05），见表3。与B组比较，A组镇痛泵按压次数明显减少，有效按压次数明显增多（P < 0.05），见表4。
表 3 2组孕产妇分娩镇痛期间补救措施比例 [n（%）]Table 3. The proportion of rescue measures during labor analgesia in two groups of parturients [n（%）]组别 n 主动补救比例 被动补救比例 A组 96 25（26.0） 21（21.8） B组 95 4（4.2） 41（43.2） χ2 16.017 8.918 P < 0.001*** 0.003** ** P < 0.01； *** P < 0.001。 表 4 2组孕产妇分娩镇痛期间镇痛泵使用情况比较 [n（%）]Table 4. Comparison of analgesia pump usage between two groups of parturients during labor analgesia [n（%）]组别 例数 有效按压
次数无效按压
次数有效按压次数比例（%） 100 33.3 50 60 66.6 75.0 A组 96 1.88 ±0.85 1.62 ±0.58 72 （75.0） 0 0 0 24（2.0） 0 B组 95 2.67 ±1.33 1.94 ±0.68 53 （55.8） 2 （2.1） 19 （20.0） 3 （ 3.2） 10 （10.5） 8 （ 8.4） χ2/t 0.715 0.491 40.649 P <0.001*** 0.001** <0.001*** ** P < 0.01； *** P < 0.001。 2.3 2组孕产妇分娩镇痛期间不良反应发生率和满意度分析
2组孕产妇的不良反应，包括恶心呕吐、瘙痒、眩晕、尿潴留等发生率差异均无统计学意义（P > 0.05），见表5。2组产妇满意度对比差异无统计学意义（P > 0.05），见表6。
表 5 2组孕产妇分娩镇痛期间不良反应发生率比较 [n（%）]Table 5. Comparison of adverse reaction rates during labor analgesia between two groups of parturients [n（%）]组别 n 恶心呕吐 瘙痒 眩晕 尿潴留 A组 96 1（1.0） 1（1.0） 0（0.0） 0（0.0） B组 95 2（2.0） 1（1.0） 0（0.0） 0（0.0） χ2 Nap P Nap Nap：P值不可计算（样本量不足）。 表 6 2组孕产妇分娩镇痛体验满意度比较 [n（%）]Table 6. Comparison of satisfaction with labor analgesia between two groups of parturients [n（%）]组别 n 满意 较满意 不满意 A组 96 81（84.0） 15（15.7） 0（0.0） B组 95 76（80.0） 16（16.8） 3（3.0） χ2 3.186 P 0.203 3. 讨论
3.1 智能化信息化管理的整体优势
国内正在开展临床应用并大力推广的智能化患者自控镇痛（ Artificial Intelligent PCA，Ai－PCA） 无线镇痛管理系统（Wireless Analgesia Management System，WAMS）[8]。智能化信息化的产科镇痛管理系统能够自动从医院的HIS系统中提取产妇的医疗病历、体检报告等诸多资料，同时也从无线控制的镇痛设备收集设备工作状况和患者自行操作的次数等数据，并对这些消息进行汇总显示。基于该数据集成，系统达到了智能运作水平，当监测到的数据超越正常范围时，能通过发出声音告警的方式，通知医护人员迅速介入处理，极大缩短患者的等候时长。有研究文献[9]指出，可以通过远程监控发现并及时处理镇痛过程中出现的问题，这是无线远程镇痛装置最显著的优点。应用这项系统，能够增加产妇与麻醉医生之间的有效沟通，这可能在某种程度上减少患者不安和焦虑的感受，进而提高整个生产过程的舒适度，有文献表明积极心理干预对接受分娩镇痛产妇可提升其对分娩镇痛的满意率[10]。
本研究结果表明，分娩镇痛智能化信息化管理系统与传统分娩镇痛管理模式相比，待产妇女子宫口全开时的NRS评分显著降低，NRS疼痛程度大于或等于7分的患者占比显著降低。可能的原因有：（1）通过智能化信息化管理系统，麻醉科医生获取待产妇女反馈实时的疼痛状态，对于NRS疼痛评分≥4分或10 min内进行镇痛泵无效按压次数>2次的待产妇女进行临床评估后给予主动补救方案，及时遏制了疼痛的进一步加重，待产妇女能够得到有效的休息，继而患者对镇痛泵的无效按压次数同时减少；（2）及时动态全方位地了解待产妇女对电子镇痛泵的按压次数和有效按压次数，麻醉科医生及时有效到场评估，判断后给予主动补救方案，如果是孕产妇或其家属对镇痛泵的误操作，则对待产妇女及其家属进行耐心的解释和合理的宣教；（3）对于电子镇痛泵故障，能够及时有效的发现，并做出相应的处理。而对照组（B组）在出现上述一系列复杂情况时，只能通过床旁按钮呼叫系统告知助产士，继而转告麻醉科医生，这一过程，需要漫长的等待，甚至错过疼痛救助的黄金时期，待产妇女得不到有效的休息继而对照组（B组）无效按压次数可能多由于未能得到及时的关注而做出的反射性动作。
3.2 与既往研究结果对比
在镇痛过程中患者的满意度方面，分娩镇痛智能化信息化管理系统未显示出明显的优势，这与在此前类似的文章研究结果不完全一致[11]，关于患者满意度的差异可能有以下几种原因：（1）实验样本量不足；（2）该实验分娩镇痛满意度只涉及（2:满意、1:较满意、0:不满意）3种评分，导致产妇评价范围相对窄，满意度无法细致的进行表达；（3）产妇满意度除涉及分娩镇痛外，还与住院期间的导乐、医疗人员态度、环境以及医保报销政策、孕产妇医疗付费方式相关[12]，产妇对疼痛控制的满意度则与她们的自主权和控制感有关[13]。此类因素在本文章未能体现。本研究结果未表明分娩镇痛智能化信息化管理相比传统管理模式不良反应发生率没有统计学差异，可能有以下几种原因：（1）分娩镇痛不良反应的发生多于镇痛泵内药物浓度有关，分娩镇痛药物不同浓度的镇痛效果及对母婴的影响不尽相同[14]；（2）由于实验样本量不足，未能记录更多的不良反应。例如硬膜外镇痛可能会延长第一产程[15]，增加产程发热的发生率[16]。
3.3 文章的局限性与总结
本研究存在一些不足之处，虽为随机对照研究，2组待产妇女的一般资料虽然差异无统计学意义，但由于是历史前后对照比较，无法做到3盲，存在人为因素造成的偏倚、混杂偏倚等影响研究结果的可靠性。此外在实验组中，有待产妇女在分娩镇痛期间，NRS疼痛评分>7分，这也进一步说明了临床工作的运行，不仅需要智能化信息化管理的帮助，还需要临床医生与病房护士的通力协作，标准化诊疗流程，合理调配人员安排，为安全分娩提供舒适度保障[17-18]，才能提高患者的满意度[19-20]。
综上所述，智能化信息技术在分娩镇痛管理中的应用能够显著降低产妇的分娩期间严重疼痛的发生，减少麻醉医师主动补救的频率，并证明了椎管内智能化信息PCA的安全性和有效性。尽管在不良反应和满意度方面的优势不够显著，但其在提升镇痛服务质量和优化医护工作流程方面表现出显著的潜力，具有广泛的推广价值。未来的研究可以着眼于优化药物配比和扩大对不同患者群体的应用，从而进一步提升智能化PCEA系统的临床效果。
-
图 1 B1-B6共6位教师3 a综合指数变化情况
Figure 1. Changes in the comprehensive index of 6 teachers in 3 years
表 1 教学水平评价指标体系
Table 1. Teaching performace evaluation index system
一级评价指标 二级评价指标 指标计算方法 A1课堂教学质量评分 A11 同行评价 评价总分 A12 专家督导评价 评价总分 A13 学生评价 评价总分 A2教研室教学活动参与率 A21 教研室教学活动参与率 教学活动参与次数/教学活动总次数×100% A3课程考核管理 A31 试卷规范性 每份试卷的教学进度、考试出题大纲、空白试卷及其
标准答案和评分标准、成绩单、试卷质量分析、成绩分析、
归档试卷封面等的完整度及规范性。A32 评分准确性 每份试卷评分标准是否准确、含有形成性考核分数、
形成性考核分数是否合理等。A33 试卷错误率 出错份数/试卷总份数×100% A34 批改出错率 试卷批改错误总分数/试卷总分数×100% A35 出错严重性 只要有1份试卷出错≥5分，记为严重 = 2分，不严重 = 1分。 
下载: 导出CSV
表 2 优序图法确定指标权重示意表
Table 2. Index weights by the optimal sequence diagram method
比较指标 A1 A2 A3 A4 …… An A1 0.5 0 0.5 A2 1 0.5 A3 0.5 0.5 A4 0.5 …… 0.5 An 0.5 注：1表示A2比A1优，0表示A1比A2劣，0.5表示优劣相当。
下载: 导出CSV
表 3 5位专家利用优序图法计算课堂教学质量评价指标权重结果（分）
Table 3. 5 experts used the optimal sequence diagram method to calculate the weight results of the classroom teaching quality evaluation index （points）
A1课堂教学质量评分 A11同行评分 A12专家督导评分 A13学生评分 合计 权重 A11同行评分 2.50 1.00 1.50 5.00 0.22 A12专家督导评分 4.00 2.50 4.00 10.50 0.47 A13学生评分 3.50 1.00 2.50 7.00 0.31
下载: 导出CSV
表 4 5位专家利用优序图法计算课程考核管理指标权重结果（分）
Table 4. 5 experts use the optimal sequence diagram method to calculate the weight result of the course assessment management index （points）
A3课程考核管理指标 A31试卷规范性 A32评分准确性 A33试卷错误率 A34批改出错率 A35出错严重性 合计 权重 A31试卷规范性 2.50 2.50 2.00 0.50 1.00 8.50 0.14 A32评分准确性 2.50 2.50 3.00 3.00 1.00 12.00 0.19 A33试卷错误率 3.00 2.00 2.50 3.00 2.00 12.50 0.20 A34批改出错率 4.50 2.00 2.00 2.50 2.50 13.50 0.22 A35出错严重性 4.00 4.00 3.00 2.50 2.50 16.00 0.26
下载: 导出CSV
表 5 5位专家利用优序图法计算教学水平评价指标权重结果（分）
Table 5. 5 experts used the optimal sequence diagram method to calculate the weight of the teaching level evaluation index （points）
A教学水平评价指标 A1课堂教学质量评分 A2教研室教学活动参与率 A3课程考核管理 合计 权重 A1课堂教学质量评分 2.50 3.50 3.50 9.50 0.42 A2教研室教学活动参与率 1.50 2.50 1.00 5.00 0.22 A3课程考核管理 1.50 4.00 2.50 8.00 0.36
下载: 导出CSV
表 6 7位教师教学水平评价指标的原始表（2017年1月至2020年1月）
Table 6. The original table of 7 teachers’ teaching level evaluation indicators （January 2017-January 2020）
教师代码 同行评分
均值（分）专家督导评分
均值（分）学生评分均
值（分）教研室教学活动
参与率（%）试卷
规范性（%）评分
准确性（%）试卷
错误率（%）批改
出错率（%）出错
严重性（分）B1 98.08 97.00 95.95 100.00 100.00 100.00 0.96 1.00 1.00 B2 97.10 93.00 90.67 95.83 100.00 100.00 1.20 1.10 1.00 B3 97.60 91.25 96.59 100.00 100.00 100.00 0.38 1.00 1.00 B4 96.37 89.00 91.00 100.00 100.00 100.00 4.18 2.45 1.00 B5 97.63 90.00 90.00 100.00 100.00 100.00 2.38 2.00 1.00 B6 96.12 90.00 95.04 70.83 100.00 100.00 6.46 1.59 1.00 B7* 94.00 89.00 90.00 100.00 100.00 100.00 1.72 2.00 1.00 标准值M 96.70 91.32 92.75 95.24 100.00 100.00 2.47 1.59 1.00 注：表中M为各指标的标准值（各指标平均值作为标准值），出错严重性指标中所有试卷错误分数均未≥5分的，全部记为不严重 = 1分。*B7教师是2019年就职于教研室，故B7教师的数据是2019年的数据。
下载: 导出CSV
表 7 二级评价指标的指数化结果
Table 7. Indexed results of secondary evaluation indicators
教师代码 同行
评价Y值专家督导
评价Y值学生
评价Y值教研室
活动Y值试卷
规范性Y值评分
准确性Y值*试卷
错误率Y值*批改
出错率Y值*出错
严重性Y值B1 1.01 1.06 1.03 1.05 1.00 1.00 2.57 1.59 1.00 B2 1.00 1.02 0.98 1.05 1.00 1.00 2.06 1.45 1.00 B3 1.01 1.00 1.04 1.05 1.00 1.00 6.50 1.59 1.00 B4 1.00 0.97 0.98 1.01 1.00 1.00 0.59 0.65 1.00 B5 1.01 0.99 0.97 1.05 1.00 1.00 1.04 0.80 1.00 B6 0.99 0.99 1.02 0.74 1.00 1.00 0.38 1.00 1.00 B7 0.97 0.97 0.97 1.05 1.00 1.00 1.43 0.80 1.00 注：*表示为低优指标，其余为高优指标；指数化后指数结果表示越高越好。
下载: 导出CSV
表 8 7位教师的教学水平的综合指数值
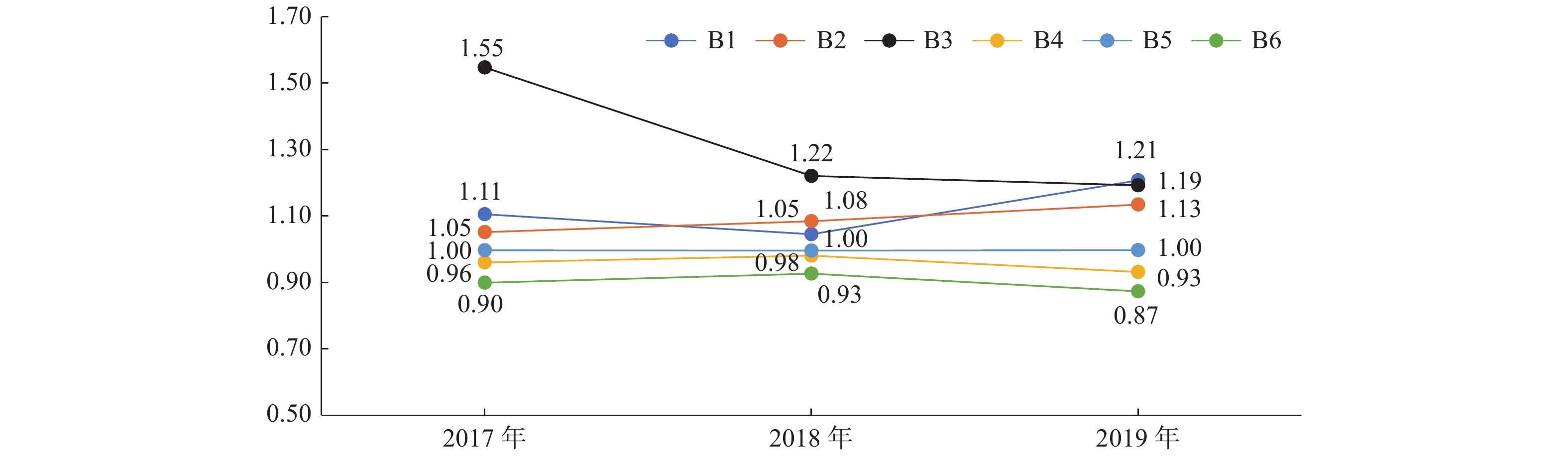
Table 8. The comprehensive index value of the teaching level of 7 teachers
教师代码 课堂教学质量评分Y值 教研室教学活动率Y值 课程考核管理Y值 综合指数 教学水平排名 B1 1.04 1.05 1.44 1.19 2 B2 1.00 1.01 1.31 1.11 3 B3 1.01 1.05 2.23 1.46 1 B4 0.98 1.01 0.84 0.94 6 B5 0.99 1.05 0.96 0.99 5 B6 1.00 0.74 0.88 0.90 7 B7 0.97 1.05 1.04 1.01 4 注：教学水平综合指数 = 课堂教学质量评分Y值×权重值 + 教研室教学活动率Y值×权重值 + 课程考核管理Y值×权重值，如：B1教师综合指数 = 1.04×0.42 + 1.05×0.22 + 1.44×0.36 = 1.19。
下载: 导出CSV
-
[1] 王丽琼,句荣辉,罗红霞,等. 高职食品类教师评价体系的构建原则与策略[J]. 中国乳业,2020,47(7):78-82. [2] 舒寒,刘钊. 我国教学评价研究进展与反思[J]. 教育教学论坛,2015,6(39):198-199. doi: 10.3969/j.issn.1674-9324.2015.39.090 [3] 李育梅,吴俊霞. 加权综合指数法在临床科室医疗质量评价中的应用[J]. 中国病案,2017,18(10):11-16. doi: 10.3969/j.issn.1672-2566.2017.10.005 [4] Shakow D,Jellinek E M. Composite index of the Kent-Rosanoff free association test[J]. J Abnorm Psychol ,1965,70(6):403-404. doi: 10.1037/h0022749 [5] Waheed M,Lal J,Prasad G. A composite index to assess Family Welfare programme activities[J]. Popcen newsletter. Population Centre (Lucknow,India),1979,5(5):7-10. [6] Antony G M,Rao K V. A composite index to explain variations in poverty,health,nutritional status and standard of living:Use of multivariate statistical methods[J]. Public Health,2007,121(8):578-587. doi: 10.1016/j.puhe.2006.10.018 [7] 王彦霞,齐秀英. 运用TOPSIS法和综合指数法综合评价医院医疗工作质量[J]. 中国病案,2015,16(10):21-23. doi: 10.3969/j.issn.1672-2566.2015.10.010 [8] 吴艳. 基于TOPSIS法和综合指数法的大连市某医院医疗质量评价[J]. 医学与社会,2017,30(4):38-39,42. [9] 葛国曙,陈奎,葛建一,等. 基于加权综合指数法评价江苏省县(市)级综合医院医疗服务能力[J]. 中国卫生事业管理,2019,36(6):428-431. [10] 李敏,朱同玉,沈银忠. 加权综合指数法在临床科室考核中的应用与分析[J]. 中国卫生质量管理,2020,27(4):45-48. [11] 廖春贵,秦年秀,胡宝清,等. 基于GIS和加权综合指数模型的2015年广西旱灾风险暴露度评估[J]. 安徽农业科学,2017,45(8):69-73. doi: 10.3969/j.issn.0517-6611.2017.08.026 [12] 李晓静,海伦贝尔·李,赵孟赫. 加权综合指数法在贵州省生态经济评价中的应用研究[J]. 生态经济,2015,31(9):48-51. doi: 10.3969/j.issn.1671-4407.2015.09.011 [13] 黄会明,陈宁,赵匀. 应用加权综合指数法评价大学生综合素质[J]. 中国高等教育评估,2009,21(2):42-44. [14] 陈仁杰,钱海雷,阚海东,等. 水质评价综合指数法的研究进展[J]. 环境与职业医学,2009,26(6):581-584. [15] Chen L,Cen Z B,Ma W Y,et al. Application of three methods in occupational health risk assessment of automobile 4S shop.[J]. Chinese Journal of Industrial Hygiene and Occupational Diseases,2019,37(11):866-870. [16] 宋军智,苗成双. 基于层次分析法的应用型人才能力综合指数评价模型[J]. 文教资料,2019,47(5):127-129,214. doi: 10.3969/j.issn.1004-8359.2019.05.056 [17] 郭昱. 权重确定方法综述[J]. 农村经济与科技,2018,29(8):252-253. doi: 10.3969/j.issn.1007-7103.2018.08.171 [18] 范丽敏,张鸿鑫,邓丽金,等. 优序图法确定护理硕士专业学位研究生培养目标体系的应用研究[J]. 中国当代医药,2019,26(35):221-224,235. doi: 10.3969/j.issn.1674-4721.2019.35.065 [19] 邢振芝,马应芳,周兰平,等. 规范化集体备课对提高课堂教学质量的影响[J]. 昆明医科大学学报,2017,38(1):138-141. doi: 10.3969/j.issn.1003-4706.2017.01.031 [20] 王一任,孙振球. 医用综合评价方法研究进展[J]. 中南大学学报(医学版),2005,30(2):228-232. [21] 金新政,厉岩. 优序图和层次分析法在确定权重时的比较研究及应用[J]. 中国卫生统计,2001,18(2):55-56. [22] 孙艳春,赵文兰,于建云,等. 昆明医学院教学质量监控状况调查研究[J]. 昆明医学院学报,2011,32(9):118-121. [23] 高璟. 新时代地方高校教学质量评价体系构建探索[J]. 科技风,2021,33(8):42-43. [24] 曹成茂, 孙福, 秦宽. 谈高校理论课教学质量评价体系构建与实践[J]. 教育教学论坛,2021,108(4):98-102. [25] 王灵芝, 周戈耀, 雷雪, 等. 基于TOPSIS法和综合指数法的贵州省中药民族药企业可持续发展能力综合评价研究[J]. 中国卫生事业管理,2021,38(1):29-33. [26] 李慧明, 候林丽, 徐鹏. 不同水质指数法在峡江水库水质评价中的应用[J]. 人民长江,2020,51(S2):32-36,87. [27] 夏焕清, 霍秀秀. 基于模糊综合指数法的嘉陵江汉中段水质评价[J]. 陕西水利,2020,88(12):96-99. [28] 乔肖翠, 李雪, 刘琰. 2种方法在典型岩溶区地下水质量评价中的对比—以地苏地下河为例[J]. 环境工程技术学报,2021,11(2):291-297. [29] 王建伟, 王小芹, 王素珍, 等. 基于TOPSIS与综合指数法的医院医疗质量综合评价[J]. 中国病案,2020,21(11):75-78. [30] 刘亚柯, 袁雪, 王鹏莉, 等. TOPSIS法和综合指数法评价郑州市基本公共卫生服务[J]. 中国公共卫生管理,2019,35(2):145-148. -
下载:
点击查看大图
计量
- 文章访问数: 3521
- HTML全文浏览量: 1714
- PDF下载量: 7
- 被引次数: 0
